4.2 SERIE NUMÉRICA Y CONVERGENCIA PRUEBA DE LA RAZÓN (CRITERIO DE D´ALEMBERT)

Como un conjunto, que contiene los miembros (también llamados elementos o términos ), y el número de términos (posiblemente infinita) se llama la longitud de la secuencia. A diferencia de un conjunto, el orden importa, y exactamente los mismos elementos pueden aparecer varias veces en diferentes posiciones en la secuencia. Una secuencia es una discreta función.Por ejemplo, (C, R, Y) es una secuencia de letras que difiere de (Y, C, R), como las cuestiones de pedido. Las secuencias pueden ser finitos, como en este ejemplo, o infinita, como la secuencia de todos, incluso positivos enteros (2, 4, 6 ,…). secuencias finitos se conocen como cadenas o palabras y secuencias infinitas como los arroyos. La secuencia vacía () se incluye en la mayoría de las nociones de secuencia, pero pueden ser excluidos en función del contexto.

Criterio de D'Alembert 

Sea una serie , tal que a_k > 0 ( serie de términos positivos).

Si existe

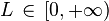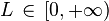con , el Criterio de D'Alembert establece que:

• si L < 1, la serie converge.
• si L > 1, entonces la serie diverge.
• si L = 1, no es posible decir algo sobre el comportamiento de la serie.

En este caso, es necesario probar otro criterio, como el criterio de Raabe.

Criterio de Cauchy 

Sea una serie , tal que a_k > 0 (serie de términos positivos). Y supongamos que existe

, siendo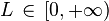 

Entonces, si:

• L < 1, la serie es convergente.
• L > 1 entonces la serie es divergente.
• L=1, no podemos concluir nada a priori y tenemos que recurrir al criterio de Raabe, o de comparación, para ver si podemos llegar a alguna conclusión.