CALCULO INTEGRAL: 4.1 SERIES

Una sucesión es un conjunto de términos formados según una ley o regla determinada.Una serie es la suma indicada de los términos de una sucesión.
EJEMPLO:
1+4+9+16+25
Cuando el numero de términos de una sucesión o serie es finita. Cuando el número de términos es ilimitado, la sucesión o serie se llama una sucesión infinita o una serie finita, en términos generales el término enésimo es una expresión que indica la ley de formación de los términos.
4.1.1 SERIES FINITAS

x i = 0

para todo

i > n

y i = 0

para todo

i > m

. En este caso el producto de Cauchy de $\sum x_i$ y $\sum y_i$ se verifica es $(x_0+\cdots + x_n)(y_0+\dots+y_m)$ . Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.

4.1.2 SERIES INFINITAS

Primer ejemplo. Para alguna $a,b\in\mathbb{R}$ , sea $x_n = a^n/n!\,$ y $y_n = b^n/n!\,$ . Entonces

$C(x,y)(n) = \sum_{i=0}^n\frac{a^i}{i!}\frac{b^{n-i}}{(n-i)!} = \frac{(a+b)^n}{n!}$

por definición y la fórmula binomial. Dado que, formalmente, 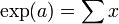$\exp(a) = \sum x$ y $\exp(b) = \sum y$ , se ha demostrado que $\exp(a+b) = \sum C(x,y)$ . Como el límite del producto de Cauchy de dos series absolutamente convergentes es igual al producto de los límites de esas series, se ha demostrado por lo tanto la fórmula

exp(a + b) = exp(a)exp(b)

para todo $a,b\in\mathbb{R}$ .

Segundo ejemplo. Sea $x (n) = 1$ para todo $n\in\mathbb{N}$ . Entonces $C (x, x)(n) = n + 1$ para todo $n\in\mathbb{N}$ por lo tanto el producto de Cauchy $\sum C(x,x) = (1,1+2,1+2+3,1+2+3+4,\dots)$ y no es convergente.

CALCULO INTEGRAL

martes, 10 de julio de 2012

4.1 SERIES

No hay comentarios:

Publicar un comentario