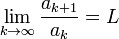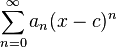4.1 SERIES
4.1.1 FINITA
4.1.2 INFINITA
4.2 SERIE NUMÉRICA Y CONVERGENCIA PRUEBA DE LA RAZÓN (CRITERIO DE D´ ALEMBERT) Y PRUEBA DE LA RAÍZ (CRITERIO DE CAUCHY)
4.3 SERIE DE POTENCIAS
4.4 RADIO DE CONVERGENCIA
4.5 SERIE DE TAYLOR
4.6 REPRESENTACIÓN DE FUNCIONES MEDIANTE LA SERIE DE TAYLOR
4.7 CALCULO DE INTEGRALES, FUNCIONES EXPRESADAS COMO SERIE DE TAYLOR
CALCULO INTEGRAL
martes, 10 de julio de 2012
4.1 SERIES
Una sucesión es un conjunto de términos formados según una ley o regla determinada.Una serie es la suma indicada de los términos de una sucesión.
EJEMPLO:
1+4+9+16+25
Cuando el numero de términos de una sucesión o serie es finita. Cuando el número de términos es ilimitado, la sucesión o serie se llama una sucesión infinita o una serie finita, en términos generales el término enésimo es una expresión que indica la ley de formación de los términos.
4.1.1 SERIES FINITAS
por definición y la fórmula binomial. Dado que, formalmente,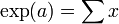 y
y  , se ha demostrado que
, se ha demostrado que  . Como el límite del producto de Cauchy de dos series absolutamente convergentes es igual al producto de los límites de esas series, se ha demostrado por lo tanto la fórmula exp(a + b) = exp(a)exp(b) para todo
. Como el límite del producto de Cauchy de dos series absolutamente convergentes es igual al producto de los límites de esas series, se ha demostrado por lo tanto la fórmula exp(a + b) = exp(a)exp(b) para todo  .
.
EJEMPLO:
1+4+9+16+25
Cuando el numero de términos de una sucesión o serie es finita. Cuando el número de términos es ilimitado, la sucesión o serie se llama una sucesión infinita o una serie finita, en términos generales el término enésimo es una expresión que indica la ley de formación de los términos.
4.1.1 SERIES FINITAS
xi = 0 para todo i > n y yi = 0 para todo i > m. En este caso el producto de Cauchy de  y
y  se verifica es
se verifica es  . Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.
. Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.
 y
y  se verifica es
se verifica es  . Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.
. Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.
4.1.2 SERIES INFINITAS
- Primer ejemplo. Para alguna
 , sea
, sea  y
y  . Entonces
. Entonces
por definición y la fórmula binomial. Dado que, formalmente,
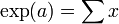 y
y  , se ha demostrado que
, se ha demostrado que  . Como el límite del producto de Cauchy de dos series absolutamente convergentes es igual al producto de los límites de esas series, se ha demostrado por lo tanto la fórmula exp(a + b) = exp(a)exp(b) para todo
. Como el límite del producto de Cauchy de dos series absolutamente convergentes es igual al producto de los límites de esas series, se ha demostrado por lo tanto la fórmula exp(a + b) = exp(a)exp(b) para todo  .
.- Segundo ejemplo. Sea x(n) = 1 para todo
 . Entonces C(x,x)(n) = n + 1 para todo
. Entonces C(x,x)(n) = n + 1 para todo  por lo tanto el producto de Cauchy
por lo tanto el producto de Cauchy  y no es convergente.
y no es convergente.
4.2 SERIE NUMÉRICA Y CONVERGENCIA PRUEBA DE LA RAZÓN (CRITERIO DE D´ALEMBERT)
Como un conjunto, que contiene los miembros (también llamados elementos o términos ), y el número de términos (posiblemente infinita) se llama la longitud de la secuencia. A diferencia de un conjunto, el orden importa, y exactamente los mismos elementos pueden aparecer varias veces en diferentes posiciones en la secuencia. Una secuencia es una discreta función.Por ejemplo, (C, R, Y) es una secuencia de letras que difiere de (Y, C, R), como las cuestiones de pedido. Las secuencias pueden ser finitos, como en este ejemplo, o infinita, como la secuencia de todos, incluso positivos enteros (2, 4, 6 ,…). secuencias finitos se conocen como cadenas o palabras y secuencias infinitas como los arroyos. La secuencia vacía () se incluye en la mayoría de las nociones de secuencia, pero pueden ser excluidos en función del contexto.
Sea una serie
Criterio de D'Alembert
Sea una serie  , tal que ak > 0 ( serie de términos positivos).
, tal que ak > 0 ( serie de términos positivos).
Si existe
con 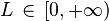 , el Criterio de D'Alembert establece que:
, el Criterio de D'Alembert establece que:
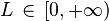 , el Criterio de D'Alembert establece que:
, el Criterio de D'Alembert establece que:- si L < 1, la serie converge.
- si L > 1, entonces la serie diverge.
- si L = 1, no es posible decir algo sobre el comportamiento de la serie.
En este caso, es necesario probar otro criterio, como el criterio de Raabe.
Criterio de Cauchy
Sea una serie  , tal que ak > 0 (serie de términos positivos). Y supongamos que existe
, tal que ak > 0 (serie de términos positivos). Y supongamos que existe
 , tal que ak > 0 (serie de términos positivos). Y supongamos que existe
, tal que ak > 0 (serie de términos positivos). Y supongamos que existe![\lim_{k \rightarrow \infty} \sqrt [k] {a_k}=L](http://upload.wikimedia.org/math/9/f/9/9f9c8260d0ee84308bde583dc2ca8991.png) , siendo
, siendo 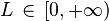
Entonces, si:
- L < 1, la serie es convergente.
- L > 1 entonces la serie es divergente.
- L=1, no podemos concluir nada a priori y tenemos que recurrir al criterio de Raabe, o de comparación, para ver si podemos llegar a alguna conclusión.
4.3 SERIE DE POTENCIAS
A partir de serie de potencias se pueden obtener otras series de potencias mediante la diferenciación e integración.En esta sección donde se aprenderá que si R (donde R diferente 0) es el radio de convergencia de una serie de potencias que define una función f, entonces f es diferenciable en el intervalo abierto (-R,R)y la derivada f pueda obtenerse al diferenciar la serie de potencia término a término.Además, se mostrara que f es integrable en todo subintervalo cerrado de (-R,R), y la integral de f se obtiene al integrar la serie de potencias término a término.Primero, se establecerán dos teoremas preliminares.
Series De Potencia Series de potencias Convergencia de las series de potencias Definición Recibe el nombre de serie de potencias toda serie de la forma ∞Σ n=0 an(x−c)n. El número real an se denomina coeficiente n-ésimo de la serie de potencias (obsérvese que el término n-ésimo de la serie es an(x−c)n). Si los coeficientes a0, a1, am−1 son nulos, la serie suele escribirse ∞Σ n=m an(x−c)n. En cierto modo, se trata de una especie de polinomio con infinitos términos. Vamos a ver que las funciones definidas como suma de una serie de potencias comparten muchas propiedades con los polinomios. ¿Para qué valores de x converge una serie de potencias? Obviamente, es segura la convergencia para x =c, con suma a0, y puede suceder que éste sea el único punto en el que la serie converge. Fuera de este caso extremo, la situación es bastante satisfactoria: veamos algunos ejemplos. Ejemplos. a) La serie geométrica ∞Σ n=0 xn converge (absolutamente) si y solo si x “ (−1,1) (con suma 11−x , como sabemos).
Series De Potencia Series de potencias Convergencia de las series de potencias Definición Recibe el nombre de serie de potencias toda serie de la forma ∞Σ n=0 an(x−c)n. El número real an se denomina coeficiente n-ésimo de la serie de potencias (obsérvese que el término n-ésimo de la serie es an(x−c)n). Si los coeficientes a0, a1, am−1 son nulos, la serie suele escribirse ∞Σ n=m an(x−c)n. En cierto modo, se trata de una especie de polinomio con infinitos términos. Vamos a ver que las funciones definidas como suma de una serie de potencias comparten muchas propiedades con los polinomios. ¿Para qué valores de x converge una serie de potencias? Obviamente, es segura la convergencia para x =c, con suma a0, y puede suceder que éste sea el único punto en el que la serie converge. Fuera de este caso extremo, la situación es bastante satisfactoria: veamos algunos ejemplos. Ejemplos. a) La serie geométrica ∞Σ n=0 xn converge (absolutamente) si y solo si x “ (−1,1) (con suma 11−x , como sabemos).
Una serie de potencias alrededor de x=0 es una serie de la forma:
Una serie de potencias alrededor de x=c es una serie de la forma:
En el cual el centro es c, y los coeficientes an son los términos de una sucesion.
4.4 RADIO DE CONVERGENCIA
En matemáticas según el teorema de Cauchy-Hadamard el radio de convergencia de una serie de la forma  , con
, con  , viene dado por la expresión:
, viene dado por la expresión:
 , con
, con  , viene dado por la expresión:
, viene dado por la expresión:
Si nos limitamos al conjunto de los números reales una serie de la forma  , con
, con  , recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r,x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0. Si lo hace para cualquier valor de x, r =
, recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r,x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0. Si lo hace para cualquier valor de x, r = 
 , con
, con  , recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r,x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0. Si lo hace para cualquier valor de x, r =
, recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r,x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0. Si lo hace para cualquier valor de x, r = 
Ejemplos
Mostraremos el radio de convergencia de algunos desarrollos en series de potencias con sus respectivos radios de convergencia sin justificar porqué el radio de convergencia es el dado.
RADIO DE CONVERGENCIA FINITO
La función 1 / (1 − x) en su desarrollo con centro 0, o sea, en series de potencia x − x0 = x − 0 = x, tiene el siguiente aspecto:
 .
.
(para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es r = 1. Eso significa que para calcular si tomo cualquier valor cuya distancia al x0 = 0 es menor que r = 1, por ejemplo el x = 0.25, entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho
 .
.
(la cuenta se puede hacer por serie de potencia). Y por otro lado
 .
.
Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el x = 2, los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia). Efectivamente:
 .
.4.5 SERIE DE TAYLOR
Una serie de potencias de x convergente se adapta bien al propósito de calcular el valor de la función que representa para valores pequeños de x (próximos a cero).Ahora deduciremos un desarrollo de potencias de x-a, siendo a un número fijo.La serie que así se obtiene se adapta al objeto de calcular la función que representa para valores de x cercanos a a.


La serie de Taylor se basa en ir haciendo operaciones según una ecuación general y mientras mas operaciones tenga la serie mas exacto será el resultado que se esta buscando. Dicha ecuación es la siguiente:

o expresado de otra forma

Donde n! es el factorial de n
f(n) es la enésima derivada de f en el punto a
Como se puede observar en la ecuación, hay una parte en la cual hay que desarrollar un binomio (x-a) n por lo que para simplificar el asunto se igualara a a siempre a 0. Para fines prácticos no afecta mucho en el resultado si se hacen muchas operaciones en la serie.
no afecta mucho en el resultado si se hacen muchas operaciones en la serie.
Teorema de Taylor: Si la función f y sus primeras n+1 derivadas son continuas en un intervalo que contiene a a y a x, entonces el valor de la función en un punto x está dado por:
La expansión en series de Taylor de n-ésimo orden debe ser exacta para un polinomio de n-ésimo orden.
Para otras funciones continuas diferenciables, como las exponenciales o sinusoidales, no se obtiene una estimación exacta mediante un número finito de términos.
El valor práctico de las series de Taylor radica en el uso de un número finito de términos que darán una aproximación lo suficientemente cercana a la solución verdadera para propósitos prácticos.
4.6 REPRESENTACIÓN DE FUNCIONES MEDIANTE LA SERIE DE TAYLOR
En matemáticas, una serie de Taylor de una función f(x) infinitamente derivable (real o compleja) definida en un intervalo abierto (a-r, a+r).
Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor.Si a = 0, a la serie se le llama serie de Maclaurin.Esta representación tiene tres ventajas importantes:La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.Se puede utilizar para calcular valores aproximados de la función.Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.Definición:
La serie de Taylor de una función f de números reales o complejos que es infinitamente diferenciable en un entorno de números reales o complejos a, es la serie de potencias que puede ser escrito de una manera más compacta como donde n! es el factorial de n y f (n)(a) denota la n-ésima derivada de f en el punto a; la derivada cero de f es definida como la propia f y (x − a)0 y 0! son ambos definidos como uno.
Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor.Si a = 0, a la serie se le llama serie de Maclaurin.Esta representación tiene tres ventajas importantes:La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.Se puede utilizar para calcular valores aproximados de la función.Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.Definición:
La serie de Taylor de una función f de números reales o complejos que es infinitamente diferenciable en un entorno de números reales o complejos a, es la serie de potencias que puede ser escrito de una manera más compacta como donde n! es el factorial de n y f (n)(a) denota la n-ésima derivada de f en el punto a; la derivada cero de f es definida como la propia f y (x − a)0 y 0! son ambos definidos como uno.
Suscribirse a:
Entradas (Atom)